1#1.1 Mô phỏng công thức dạng ax+b=0

Bây giờ chúng ta thử nhìn vào hình sau:

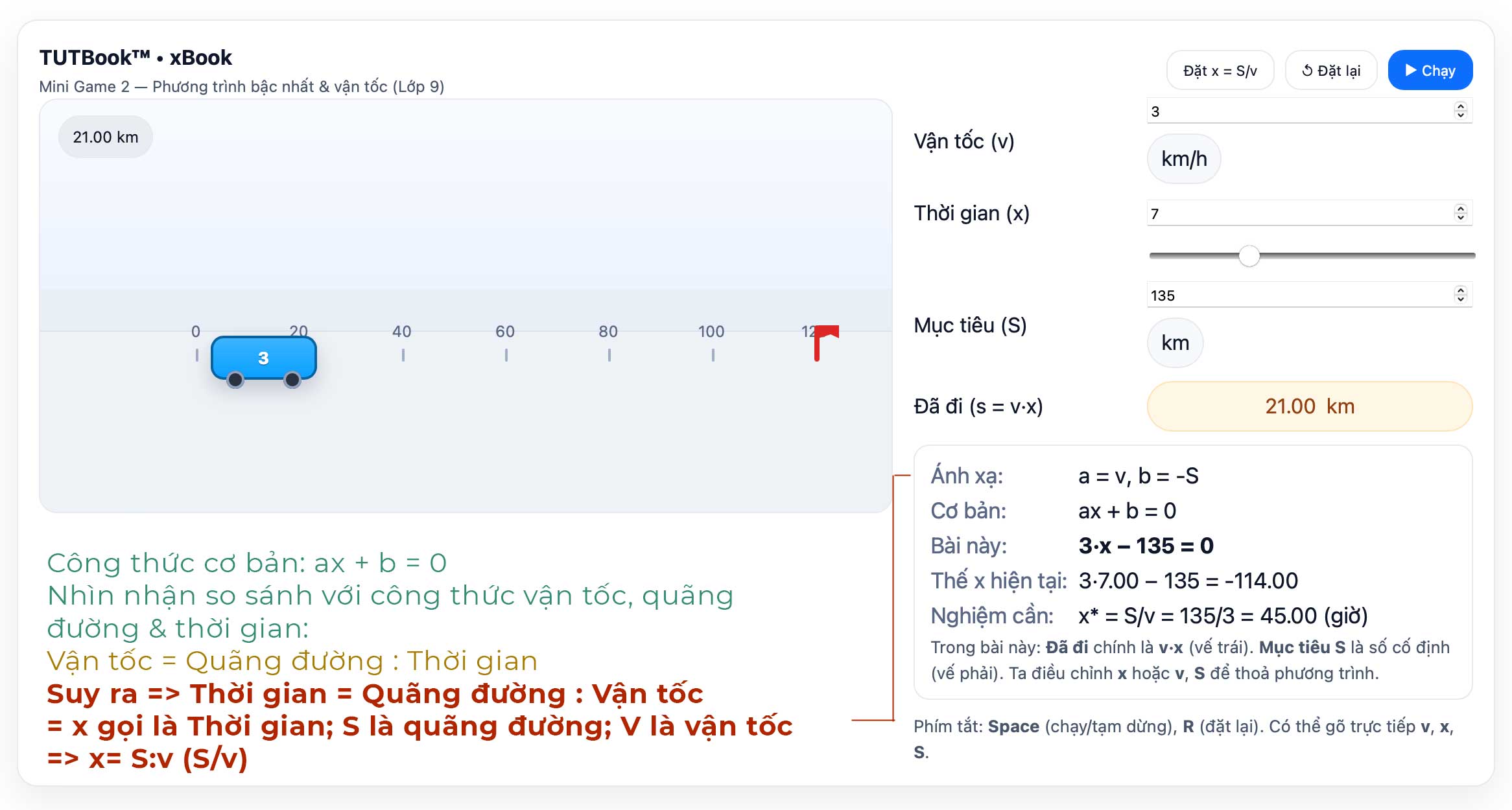
Hãy xem mô phỏng sau:

Hãy xem các mô phỏng khác ở phần tiếp theo

Tổng kết lại ( dành cho các bạn muốn tìm hiểu kỹ thêm ):

1) Bài toán và mục tiêu

• • Cho vận tốc v (km/h), cần tìm thời gian x (giờ) để đi được đúng quãng đường mục tiêu S (km).

  • Câu hỏi: Khi nào xe đạt đích? → khi quãng đường đã đi bằng mục tiêu.

2) Mô hình hóa (đặt ẩn, xác định đại lượng)

• • Đại lượng cần tìm: x (thời gian) → ẩn số.

  • Đại lượng đã biết: v (vận tốc), S (mục tiêu).

  • Quãng đường đã đi sau thời gian x: s = v · x.
    ⟹ Ở bài này, “Đã đi” chính là vế trái của phương trình.

3) Lập phương trình từ tình huống

• • Điều kiện “đạt đích”: s = S ⟹ v · x = S.

  • Đưa về một vế để nhìn đúng dạng bậc nhất:
    v · x − S = 0.

4) Đối chiếu với dạng chuẩn $ax + b = 0$

• • So sánh: v · x − S = 0 ↔ a = v, b = −S.

  • Ẩn số là x.

  • Công thức nghiệm:

    $x = -dfrac{b}{a} = dfrac{S}{v}$x=−ab​=vS​.

Ví dụ:

$v=40$

v=40 km/h,

$S=120$

S=120 km ⇒

$x = 120/40 = 3$

x=120/40=3 (giờ).

5) Diễn giải kết quả (ý nghĩa – kiểm tra nhanh)

• • Nếu x < S/v ⇒

    $v·x – S < 0$v⋅x−S<0 ⇒ chưa tới đích (mô phỏng tô màu cam).

  • Nếu x = S/v ⇒

    $v·x – S = 0$v⋅x−S=0 ⇒ vừa chạm đích (màu xanh).

  • Nếu x > S/v ⇒

    $v·x – S > 0$v⋅x−S>0 ⇒ đi quá đích (màu đỏ).

6) Cách nghĩ theo từng bước (HS tự nhận diện)

1. 1. Đang tìm gì? → thời gian x.

   2. Công thức gốc của hiện tượng? → chuyển động đều: s = v · t (ở đây t = x).

   3. Điều kiện “đạt yêu cầu”? → s = S.

   4. Gộp lại → v · x = S → chuyển vế v · x − S = 0.

   5. Khớp dạng chuẩn ax + b = 0 → a = v, b = −S.

   6. Giải ẩn → x = S/v.

   7. Kiểm tra → thay ngược vào v·x − S phải cho bằng 0.

   8. Đơn vị → v (km/h), x (h), S & s (km) phải tương thích.

7) Nhìn bằng đồ thị (mở rộng tư duy)

• • Vẽ

    $y = v x – S$

  • Nghiệm là hoành độ giao điểm với trục

    $x$ 

    $x^* = S/v$

  • $y<0$

     (dưới trục) → chưa tới;

    $y=0$

    → vừa đủ;

    $y>0$

    → vượt đích.
    (Trong mô phỏng, 3 trạng thái này chính là ba màu của “Đã đi”.)

8) Biến thể quen thuộc (đổi ẩn số)

• • Tìm v khi biết

    $x, S$x,S: v = S/x (vẫn là bài toán bậc nhất theo ẩn v).

  • Tìm S khi biết

    $v, x$v,x: S = v·x.

9) Sai sót thường gặp & cách tránh

• • Nhầm dấu b: nhớ b = −S.

  • Lẫn đơn vị: v (km/h) phải đi với x (giờ).

  • Quên kiểm tra: giải xong không thế lại để xem

    $v·x − S$v⋅x−S có bằng 0 không.