5 Sections
5 Lessons
10 Weeks

Expand all sectionsCollapse all sections

CHAPTER I. LINEAR EQUATIONS AND SYSTEMS OF LINEAR EQUATIONS
The main content of this chapter focuses on exploring and applying methods for solving problems of the form:
- Equations reducible to first-degree equations in one variable: These are equations that may seem complex at first but can be transformed into the basic form ax + b = 0 to determine the value of the variable x.
- First-degree equations in two variables and systems of two first-degree equations in two variables: These problems involve two variables (x, y) and are represented by two equations. Solving the system allows us to find both values of x and y at the same time, satisfying both equations simultaneously.
Applications and significance when learning

Mastering knowledge of first-degree equations and systems of first-degree equations is extremely important and meaningful, not only in learning but also in real-life situations:
- Solving real-life problems: Most issues, from simple to complex in life, such as calculating costs, allocating resources, or determining area and volume, can be modeled and solved using equations. For example, calculating the area of a piece of land is an application of equations.
- Developing logical thinking and problem-solving skills: Learning how to set up and solve equations helps you practice analytical skills, logical thinking, and approach a problem systematically.
- A foundation for higher-level mathematics knowledge: Knowledge of first-degree equations is a solid foundation for learning more complex types of equations and inequalities later on, such as quadratic equations, exponential equations, logarithmic equations, and systems with more variables.
In summary, studying this chapter provides you with a powerful tool to solve problems, not only in Mathematics but also in many other fields of science and everyday life.
5
CHAPTER II. INEQUALITIES. LINEAR INEQUALITIES IN ONE VARIABLE
0
CHAPTER III. RADICAL EXPRESSIONS
0
CHAPTER IV. METRIC RELATIONS IN A RIGHT TRIANGLE
0
CHAPTER V. THE CIRCLE
0

Content

1#1.1 Simulation of the formula in the form ax + b = 0

Now let's take a look at the following figure:

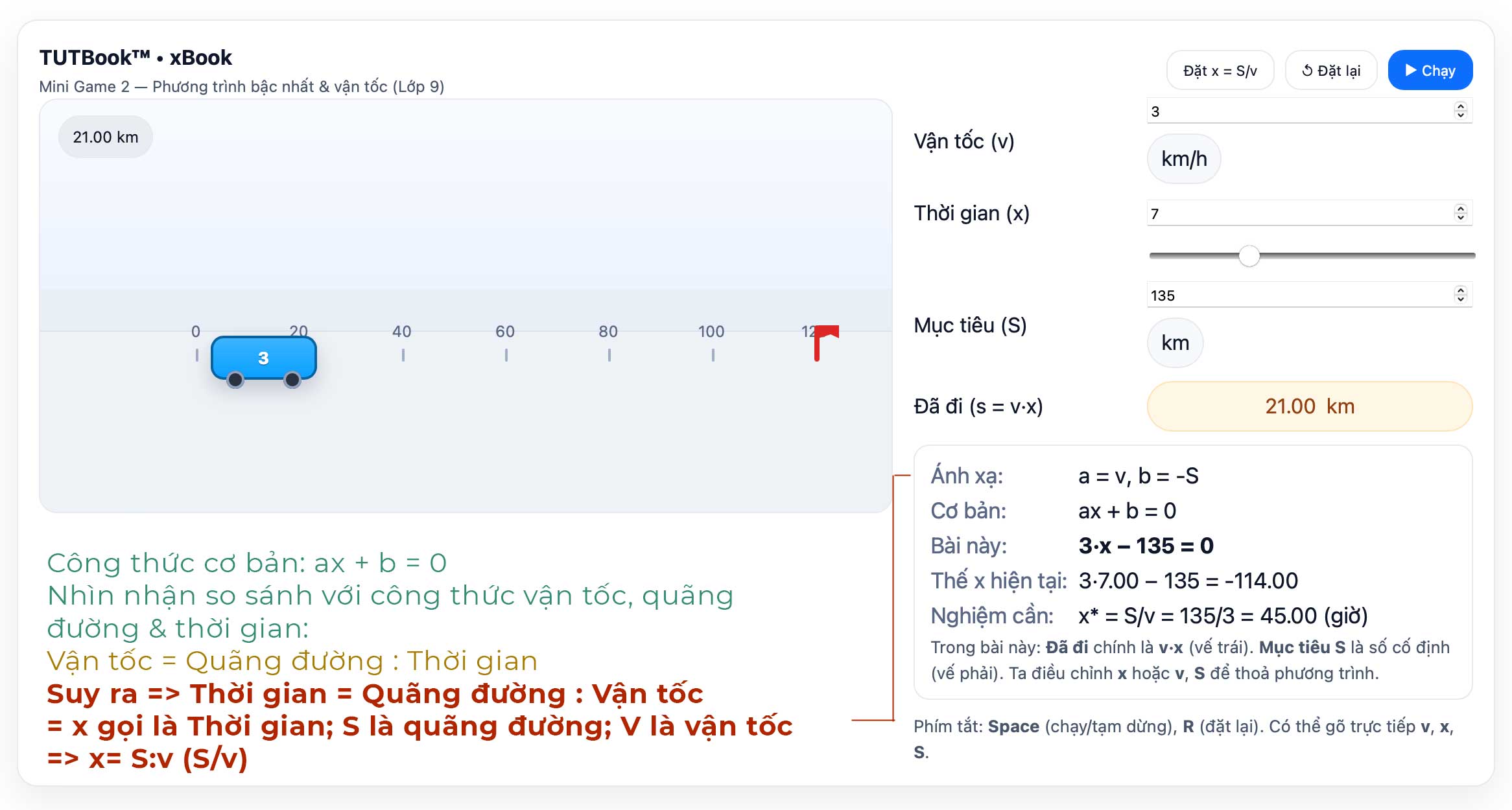
View the following simulation:

TUTBook™ • xBook

Mini Game 2 — First-degree Equation & Velocity (Grade 9)

0.00 km

Vận tốc (v)

km/h

Thời gian (x)

Mục tiêu (S)

Đã đi (s = v·x)

0.00 km

Mapping a = v, b = -S

Basic: ax + b = 0

This problem v·x − S = 0

Current x value: v·0.00 − S = −S

Required solution x* = S/v = 3.00 (giờ)

In this problem: Distance traveled = v \cdot x. Target S is a fixed number. Adjust x/v/S to satisfy the equation.

Keyboard shortcuts Space Run/Pause R (Reset ). Can type directly v, x, S.

See other simulations in the next section

In summary (for those who want to learn more in detail):

1) Problem and objective

- Given the velocity v (km/h), find the time x (hours) required to travel exactly the target distance S (km).
- Question: When does the vehicle reach the destination? → when the distance traveled equals the target.

2) Modeling (setting the variable, determining the quantities)

- Quantity to be found: x (time) to unknown variable.
- Known quantities: v (velocity), S (target).
- The Distance traveled sau thời gian x: s = v · x.
  ⟹ Ở bài này, “Đã đi” chính là vế trái của phương trình.

3) Lập phương trình từ tình huống

- Điều kiện “đạt đích”: s = S ⟹ v · x = S.
- Đưa về một vế để nhìn đúng dạng bậc nhất:
  v · x − S = 0.

4) Đối chiếu với dạng chuẩn $ax + b = 0$

- So sánh: v · x − S = 0 ↔ a = v, b = −S.
- Ẩn số là x.
- Công thức nghiệm:
  
  $x = -dfrac{b}{a} = dfrac{S}{v}$ $x = - a b = v S$ .

Example:

$v=40$

$v = 40$ km/h,

$S=120$

$S = 120$ km ⇒

$x = 120/40 = 3$

$x = 120/40 = 3$ (giờ).

5) Diễn giải kết quả (ý nghĩa – kiểm tra nhanh)

- If x < S/v ⇒
  
  $v·x – S < 0$ $v \cdot x - S < 0$ ⇒ chưa tới đích (mô phỏng tô màu cam).
- If x = S/v ⇒
  
  $v·x – S = 0$ $v \cdot x - S = 0$ ⇒ vừa chạm đích (màu xanh).
- If x > S/v ⇒
  
  $v·x – S > 0$ $v \cdot x - S > 0$ ⇒ đi quá đích (màu đỏ).

6) Cách nghĩ theo từng bước (HS tự nhận diện)

1. Đang tìm gì? → thời gian x.
2. Công thức gốc của hiện tượng? → chuyển động đều: s = v · t (ở đây t = x).
3. Điều kiện “đạt yêu cầu”? → s = S.
4. Gộp lại → v · x = S → chuyển vế v · x − S = 0.
5. Khớp dạng chuẩn ax + b = 0 → a = v, b = −S.
6. Giải ẩn → x = S/v.
7. Kiểm tra → thay ngược vào v·x − S phải cho bằng 0.
8. Đơn vị → v (km/h), x (h), S & s (km) phải tương thích.

7) Nhìn bằng đồ thị (mở rộng tư duy)

- Vẽ
  
  $y = v x – S$
- Solution là hoành độ giao điểm với trục
  
  $x$
  
  $x^* = S/v$
- $y<0$
  
  (dưới trục) → chưa tới;
  
  $y=0$
  
  → vừa đủ;
  
  $y>0$
  
  → vượt đích.
  (Trong mô phỏng, 3 trạng thái này chính là ba màu của “Đã đi”.)

8) Biến thể quen thuộc (đổi ẩn số)

- Search v khi biết
  
  $x, S$ $x, S$ : v = S/x (vẫn là bài toán bậc nhất theo ẩn v).
- Search S khi biết
  
  $v, x$ $v, x$ : S = v·x.

9) Sai sót thường gặp & cách tránh

- Nhầm dấu b: nhớ b = −S.
- Lẫn đơn vị: v (km/h) phải đi với x (giờ).
- Quên kiểm tra: giải xong không thế lại để xem
  
  $v·x − S$ $v \cdot x - S$ có bằng 0 không.

The main content of this chapter focuses on exploring and applying methods for solving problems of the form:

Applications and significance when learning

MATH 9# Volume 1 – CD – Theory

1#1.1 Simulation of the formula in the form ax + b = 0

View the following simulation:

See other simulations in the next section

In summary (for those who want to learn more in detail):

1) Problem and objective

2) Modeling (setting the variable, determining the quantities)

3) Lập phương trình từ tình huống

4) Đối chiếu với dạng chuẩn ax+b=0ax + b = 0

5) Diễn giải kết quả (ý nghĩa – kiểm tra nhanh)

6) Cách nghĩ theo từng bước (HS tự nhận diện)

7) Nhìn bằng đồ thị (mở rộng tư duy)

8) Biến thể quen thuộc (đổi ẩn số)

9) Sai sót thường gặp & cách tránh

Tìm kiếm

Login with your site account

Register a new account

Modal title

4) Đối chiếu với dạng chuẩn $ax + b = 0$